Курс экономической теории

С практической точки зрения, в том числе и для определения изменения выручки, часто бывает важно быстро установить по виду графика спроса или предложения, является ли изображенная на нем функция эластичной или нет.

Для графика предложения эта задача решается весьма просто: ответ находится исходя из того, какую ось координат пересекает изображающая линейную функцию предложения прямая (или касательная к кривой, изображающей нелинейную функцию предложения, проведенная через интересующую нас точку на этой кривой):

ε_S = (∆Q/∆P) * (P/Q) = (P/Q) : (∆P/∆Q).

Первой в полученном выражении (то есть делимым) является (рис. 6.8) величина, равная тангенсу угла наклона прямой, проведенной через данную точку из начала координат (tg а = БД/ОД = P/Q), а второй (то есть делителем) - величина, равная тангенсу угла наклона самой прямой предложения или касательной к ней в данной точке (tg b = БГ/ВГ = ∆P/∆Q).

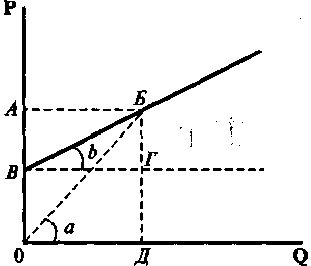
Рис. 6.8

Очевидно, что когда прямая линия предложения (или касательная к кривой) пересекает ось цен (Р), как на рис. 6.8, то угол наклона прямой (ОБ), проведенной из начала координат в нашу точку, будет больше угла наклона кривой предложения, tg a > tg b, а значит, (P/Q) > (∆P/∆Q) и ε_S > 1 - то есть предложение будет эластичным.

Если же прямая линия предложения (или касательная к кривой) пересекает ось количества (Q), то угол наклона прямой из начала координат будет меньше угла наклона кривой предложения, БГ/ОГ < БГ/ВГ, tg a < tg b, (P/Q) < (∆P/∆Q) и ε_S < 1 - предложение будет неэластичным (рис. 6.9).

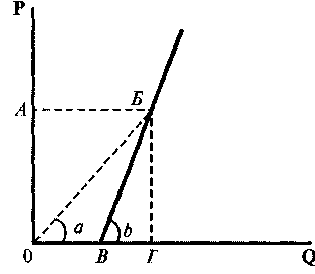
Рис. 6.9

Если же мы обратимся к графику спроса, то наша задача установления жесткости или эластичности функции спроса в данной точке будет несколько сложнее. Прежде всего надо отметить, что при поверхностном взгляде эластичность спроса часто ошибочно отождествляют с наклоном кривой спроса, что и приводит к неверным выводам. Например, можно услышать, что функция спроса с единичной эластичностью выражается прямой линией с углом наклона в 45 градусов. Наклон прямой линии действительно одинаков в любой ее точке. Тангенс угла в 45 градусов действительно равен единице. Но в формулу эластичности помимо сомножителя (∆Q/∆P), действительно неизменного и равного обратной величине наклона обратной прямой спроса, а для 45-градусного угла наклона действительно равного единице, входит и другой сомножитель – (P/Q), вот он-то как раз и меняется в зависимости от расположения интересующей нас точки даже на прямой спроса. Очевидно, что учитывать только наклон даже для линейного спроса недостаточно.

Для определения гибкости или жесткости спроса в данной точке опустим из нее перпендикуляр на горизонтальную ось координат, а саму прямую спроса (или касательную к кривой спроса) продолжим до пересечения с той же осью (рис. 6.10).

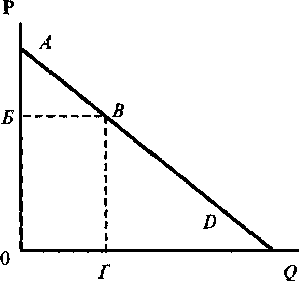
Рис. 6.10

Тогда соотношение длин отрезков ВГ/ГД будет равно по абсолютной величине соотношению (∆Р/∆Q), а обратному соотношению (∆Q/∆P) из формулы эластичности будет равно обратное соотношение (ГД/ВГ). Соотношение же БО/ОГ = ВГ/ОГ будет равно соотношению (P/Q). Таким образом, формулу ценовой эластичности спроса мы можем представить в следующем виде:

|ε| = (∆Q/∆P) * (P/Q) = (ГД/ВГ) * (ВГ/ОГ) = ГД/ОГ.

Итак, для любой точки В на кривой спроса абсолютное значение ценовой эластичности спроса определяется соотношением длин отрезков справа (ГД) и слева (ОГ) от перпендикуляра, опущенного из этой точки на горизонтальную ось координат. Если правый отрезок больше левого, то и спрос в таком случае эластичен (как на рис. 6.10); если правый отрезок меньше левого - спрос в данной точке неэластичен.

Отсюда следует, что при достаточно высоких ценах (когда правый отрезок больше левого) линейный спрос всегда эластичен, даже когда линия спроса имеет очень крутой наклон, при движении вниз вдоль прямой спроса эластичность спроса понижается, а при переходе к достаточно низким ценам (когда правый отрезок уже меньше левого) спрос при той же самой функции и на том же самом графике становится неэластичным, в том числе и при весьма пологом расположении прямой спроса или касательной к нелинейной кривой спроса на графике. Это обстоятельство мы и учитывали выше, когда рассматривали изменение выручки в результате изменения цен при различной эластичности спроса.

Если же мы остановимся ровно посередине отрезка ОД, когда О Г = ГД, то получим единственную точку на линейной кривой спроса с единичной эластичностью. Для любых точек слева от нее |ε| > 1, стремясь к бесконечности при движении вверх вдоль кривой спроса к точке пересечения линии спроса и вертикальной оси координат, а справа от нее - |ε| < 1, стремясь к нулю при движении вниз вдоль кривой спроса к точке пересечения линии спроса и горизонтальной оси координат независимо от угла наклона подобной прямой линии (рис. 6.11).

Рис. 6.11

Кроме того, величину |ε| можно определить и исходя из соотношения углов, образуемых горизонтальной осью координат с линией, проведенной через точки значения цены и количества для данной величины спроса (а), и с самой прямой спроса (или касательной к нелинейной кривой спроса) (b) (рис. 6.12).

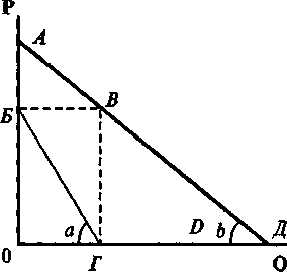
Рис. 6.12

В этом случае |ε| = |tg а|: |tg b|.

Укажем, что данное равенство также вытекает из преобразования формулы эластичности

ε^D = (∆Q^D/∆P) * (P/Q^D) = (P/Q^D) : (∆P/∆Q^D).

где / P/Q^D = tg a; ∆P/∆Q^D = tg b.

Присмотревшись к треугольникам АОД, АБВ и ВГД на рисунках 6.10, 6.11 и 6.12, можно заметить, что все они подобны. Из этого вытекают еще два способа определения абсолютного значения ценовой эластичности спроса:

|ε| = ГД/ОГ = ОБ/БА = ВД/ВА.

Проиллюстрируем это с помощью линейной функции спроса Q^D = а - bР.

По определению эластичности,

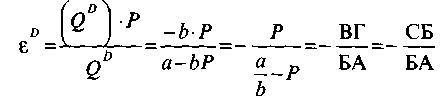
В нижней части рисунка 6.13 показана зависимость выручки от цены: R= P(Q^D) * Q^D. Это квадратичная функция, достигающая максимума, как было показано выше, в середине отрезка ОД, при единичной ценовой эластичности спроса. Из графика видно, что при эластичном спросе, то есть слева от середины линии спроса, выручка с увеличением количества и уменьшением цены растет, а при неэластичном, то есть справа от середины, - падает.

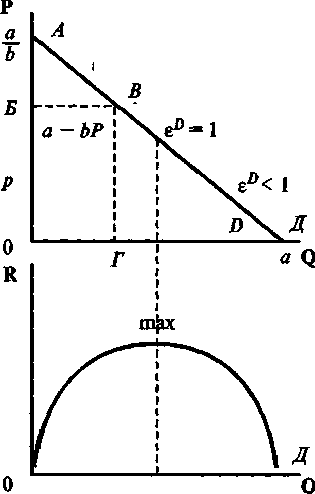
Рис. 6.13

Любой из указанных способов можно использовать в зависимости от особенностей конкретной ситуации и задач исследования.